
Moment of inertia along X-axis and Y-axis is given by, Moment of inertia along Y-axis is given by, For circular section Moment of inertia along X-axis is given by,Īnd, d is the depth of the rectangular section. The moment of inertia of the following sections will be I G = Moment of inertia of the given area about I AB = Moment of inertia of the given area along AB It states that if the moment of inertia of a plane area about an axis in the plane of area through the center of gravity of the plane area be represented by I G, then the moment of inertia of the given plane area about a parallel axis AB In the plane of area at a distance h from the C.G. The moment of inertia is also known as the polar moment of inertia. The theorem of the perpendicular axis states that if Ixx and Iyy be the moment of inertia of a plane section about two mutually perpendicular axes X-X and Y-Y in the plane of the section, then the moment of inertia of the section Izz about the Z-Z, perpendicular to the plane and passing through the intersection of X-X and Y-Y is given by
If Ak² = I, then k is known as the radius of gyration about the given axis.ĥ0+ Home designe images Theorem of the perpendicular axis Let the whole mass ( or area ) of the body is concentrated at a distance ‘k’ from the axis of reference, then the moment of inertia of the whole area about the given axis will be equal to Ak². The radius of gyration of a body ( or given lamina ) about an axis is a distance such that its square multiplied by the area gives a moment of inertia of the area about the given axis. In the imperial system, the unit is inches to the fourth power (in 4). The SI unit of the polar moment of inertia is metered to the fourth power (m 4). Where, r = distance to the element dA Units Polar moment of inertia can be mathematically represented by the given formula Polar moment of inertia is also known as second polar moment of area. Polar moment of inertia describes the cylindrical object’s resistance to torsional deformation when torque is applied in a plane that is parallel to the cross section area or in a plane that is perpendicular to the object’s central axis. Polar moment of inertia is a quantity used to predict an object’s ability to resist torsion, in objects ( or segments of objects) with an invariant circular cross section. The mass remains same and its radius is larger compare to above disc. Now, melt this disc and convert it into ring which is shown in figure Example (2) Consider a disc of radius R and mass M. If you rotate baseball by holding the handle, you have to put in more effort than when you rotate baseball by holding it at its hitting end. If the greater mass is concentrated away from the axis, then moment of inertia will be greater.įor example(1), take a baseball club. Physical significance of moment of inertia hence moment of inertia about the X-axis is represented by Iₓₓ whereas about Y-axis represents Iyy. of the area ( or mass ) from an axis is called the moment of inertia of the area ( or mass ) about that axis. The product of the area ( or mass ) and the square of the distance of the C. Moment of inertia formula Moment of inertia definition Let’s see what are they:- Moment of inertia formula Moment of inertia formula So, I have given some formula for the moment of inertia of different objects having a different geometrical shape. It depends on geometrical shape of the object like a circular, rectangular, triangular, thin rod, etc.

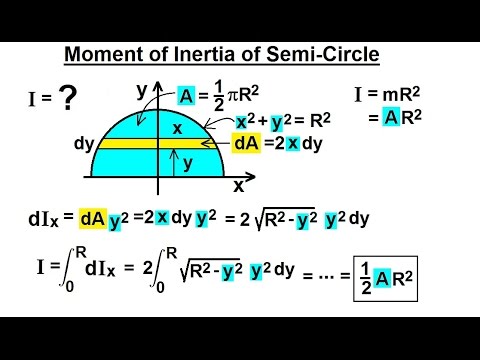
The formula for the moment of inertia is different for different shapes of the object. Numerical to calculate Moment of Inertia The formula for moment of inertia.Example (2) Consider a disc of radius R and mass M.Physical significance of moment of inertia.The dot represents a points mass, in size equal to $\frac$. I want to calculate the tensor of the moment of inertia.


 0 kommentar(er)
0 kommentar(er)
